

This idea can be generalised to any pure polarisation state: there are orthonormal (complex) transformations on the co-ordinate axes which keep the D'Alembert wave equation - see for example the Riemann-Silberstein vectors, whose Cartesian components fulfill the D'Alembert wave equation. is not a big difference, either because light either has a predominant polarisation in a constant (non spatially varying) direction (so the only significant component is a Cartesian one), or because it is a classical probabalistic mixture of pure polarisation states with such predominant, non spatially varying direction polarisation. ( Likeness) For many kinds of problem, 2. ( Difference) In co-ordinate systems other than Cartesian, the components of the electromagnetic field do not in general fulfill the D'Alembert wave equation. The propagation for linear acoustic waves is also the D'Alembert wave equation ( Likeness) The Cartesian components of the electromagnetic field vectors, as well as the Cartesian components of the potential four vector all fulfill the D'Alembert wave equation (Helmholtz equation in the time harmonic case). there is a polarisation state light that does not apply to acoustic waves.
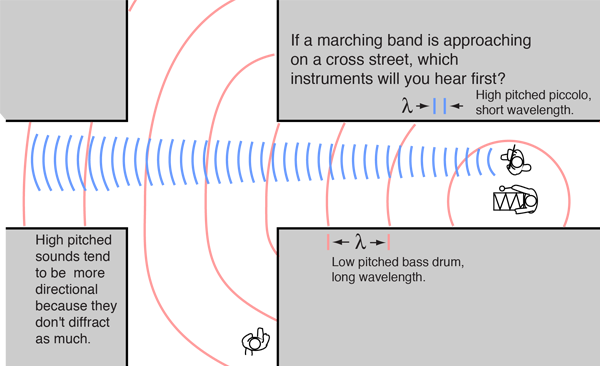
It is VERY hard to construct actual scenarios where linear acoustic diffraction differs substantially from the diffraction of light.Īs noted already, linear acoustic waves are scalar pressure fields, whereas electromagnetism is a vector phenomenon, i.e. The answer is the two are very close, but there are theoretical differences.


 0 kommentar(er)
0 kommentar(er)
